LXX's blog

实验四：主元分析

  • ~1.98K 字
  • 次阅读
  • 条评论

实验四：主元分析

主元分析函数

熟悉函数

1
2
from sklearn.decomposition import PCA
pca = PCA(n_components=2)

输入参数：

参数 意义
n_components 整数表示保留的维度数，小数表示可解释方差占比最小值

返回值：

PCA是一个类，该函数是其构造函数，因此返回的是一个对象，要使用主元分析还需要调用该类中的方法fit()

修改参数

原始数据

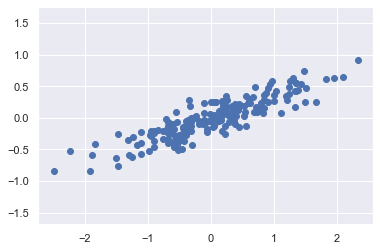
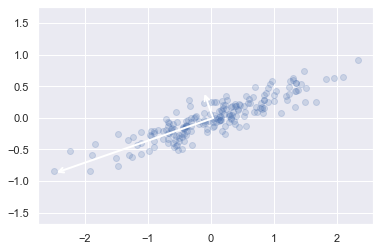
n_components=2

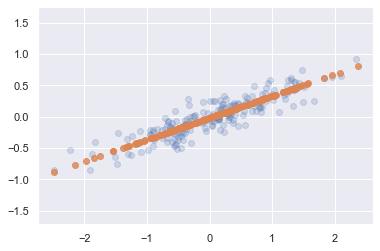
n_components=1

手写数字的 PCA 噪声去除

代码分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from sklearn.datasets import load_digits
import numpy as np
import matplotlib.pyplot as plt
digits = load_digits()  # 加载手写数字数据集

def plot_digits(data):  # 定义绘图函数
    fig, axes = plt.subplots(4, 10, figsize=(10, 4),
                             subplot_kw={'xticks':[], 'yticks':[]},
                             gridspec_kw=dict(hspace=0.1, wspace=0.1))
    for i, ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8, 8),
                  cmap='binary', interpolation='nearest',
                  clim=(0, 16))
plot_digits(digits.data)  # 绘制原始数据

np.random.seed(2333)
noisy = np.random.normal(digits.data, 4)  # 生产正态分布噪声（标准差=4）
plot_digits(noisy)

pca = PCA(0.50).fit(noisy)  # 主元分析（可解释方差比例为0.7）
pca.n_components_  # 主元数

components = pca.transform(noisy)  # 返回降维后的数据
filtered = pca.inverse_transform(components)  # 将数据转换到原始空间
plot_digits(filtered)

原始数据

加入噪声

PCA去除噪声

实验结果

在不同条件下，需要的主元个数：

需要的解释方差百分比
噪声 std 0.5 0.7 0.9
2 6 13 35
4 12 26 49
8 22 37 54
  • 噪声越大，需要的主元个数越多
  • 需要的解释方差百分比越大，需要的主元个数越多

人脸 PCA 重建

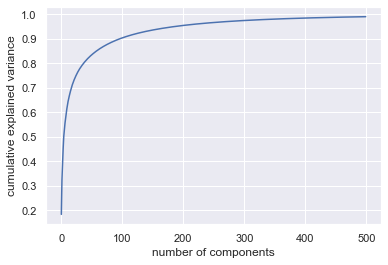
PCA的累计解释方差比与元数的关系

n_pcs 累计解释方差比
50 0.833
150 0.936
300 0.975

从图中可以看出，降到 100 维左右即可保留至少 90%的信息。

不同维度下人脸重建的效果：

人脸图像 PCA 前后识别率差别

主元数 识别率
未降维 0.39
30 0.50
50 0.50
100 0.41
150 0.29

使用如下代码生成

1
2
3
4
5
6
7
8
9
10
11
12
X = np.linspace(1, 150, 150, dtype = int)
Y = []
for x in X:
    pca = PCA(n_components = x, whiten = True, random_state = 0).fit(X_train)
    X_train_pca = pca.transform(X_train)
    X_test_pca = pca.transform(X_test)
    knn = KNeighborsClassifier(n_neighbors = 1)
    knn.fit(X_train_pca, y_train)
    Y.append(knn.score(X_test_pca, y_test))
plt.plot(X, Y)
plt.xlabel('n_components')
plt.ylabel('Test set accuracy')

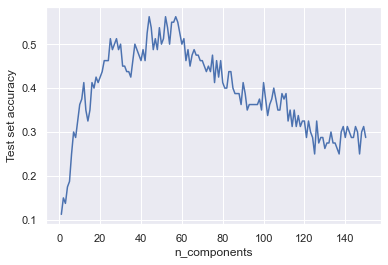
准确率与主元数关系

由该图像可以看出，主元数在 50 左右时，人脸重建后的识别率最高