实验一:KNN 与多项式回归
KNN
wine
采样率 0.3(共 42 个训练样本 11 个测试样本)
| 近邻范围 | 准确率(第一次) | 准确率(第二次) | 准确率(第三次) |
|---|---|---|---|
| 1 | 81.82% | 63.64% | 63.64% |
| 2 | 72.73% | 63.64% | 63.64% |
| 3 | 72.73% | 63.64% | 63.64% |
| 4 | 81.82% | 63.64% | 63.64% |
| 5 | 81.82% | 63.64% | 54.55% |
| 8 | 90.91% | 72.73% | 63.64% |
| 10 | 90.91% | 72.73% | 54.55% |
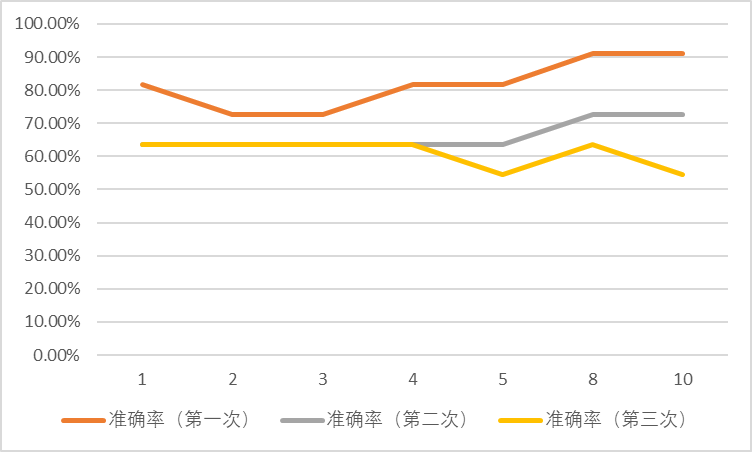
采样率 0.5(共 71 个训练样本 18 个测试样本)
| 近邻范围 | 准确率(第一次) | 准确率(第二次) | 准确率(第三次) |
|---|---|---|---|
| 1 | 66.67% | 72.22% | 77.78% |
| 2 | 66.67% | 66.67% | 83.33% |
| 3 | 61.11% | 61.11% | 83.33% |
| 4 | 55.56% | 61.11% | 72.22% |
| 5 | 66.67% | 61.11% | 77.78% |
| 8 | 72.22% | 66.67% | 72.22% |
| 10 | 72.22% | 66.67% | 77.78% |
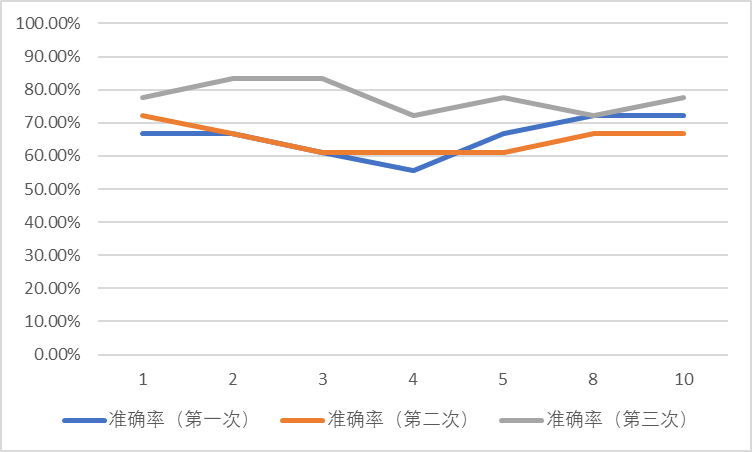
采样率 0.8(共 113 个训练样本 29 个测试样本)
| 近邻范围 | 准确率(第一次) | 准确率(第二次) | 准确率(第三次) |
|---|---|---|---|
| 1 | 65.52% | 79.31% | 51.72% |
| 2 | 65.52% | 65.52% | 55.17% |
| 3 | 62.07% | 72.41% | 62.07% |
| 4 | 62.07% | 72.41% | 58.62% |
| 5 | 65.52% | 75.86% | 58.62% |
| 8 | 62.07% | 72.41% | 72.41% |
| 10 | 62.07% | 79.31% | 75.86% |
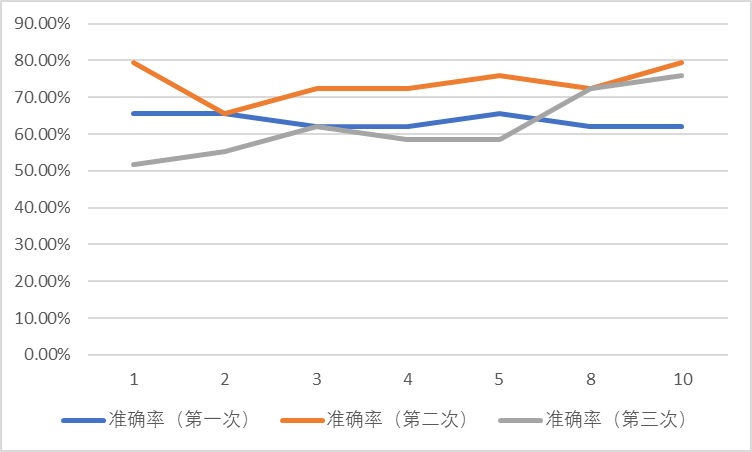
参数选取
由以上实验可知,在 K 比较小的时方差较大,K 比较大时方差较小。因此可尽量选择较大的 K,不过 K 过大会导致过拟合,所以在该实验中 K 可选取 3~5。
优化
在确定数据集合采样率后自适应选择 K 的值
1 | k = range(1,10) |
运行结果:

Regression
信号频率 1
噪声方差 0.2
M=10
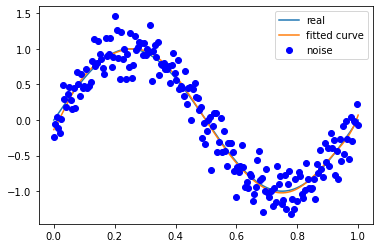
M=180
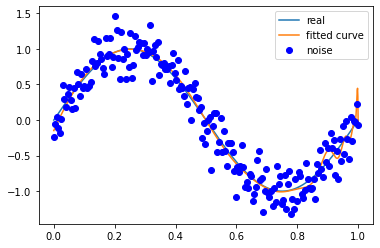
噪声方差 0.5
M=10
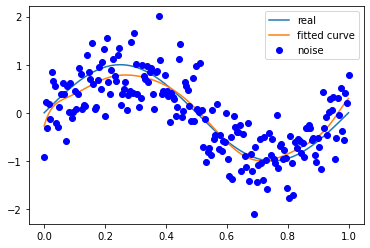
M=50
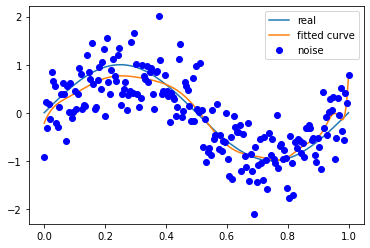
M=180
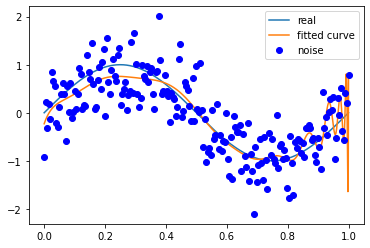
信号频率 2
噪声方差 0.5
M=10
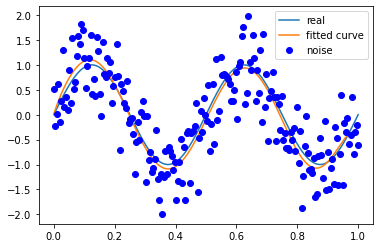
M=180
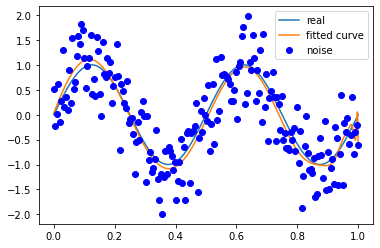
信号频率 4
噪声方差 0.2
M=10
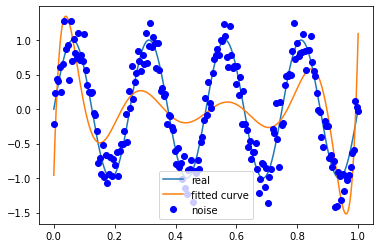
M=50
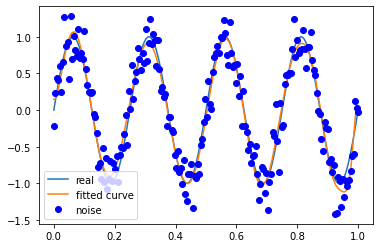
M=180
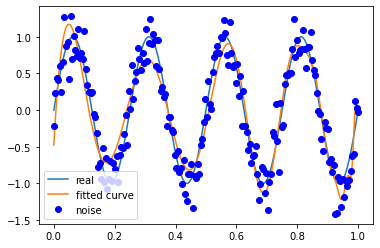
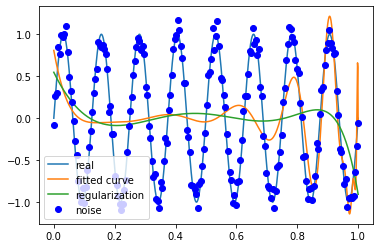
噪声方差 0.5
M=30

M=180

信号频率 8
噪声方差 0.1
M=180
噪声方差 0.5
M=180
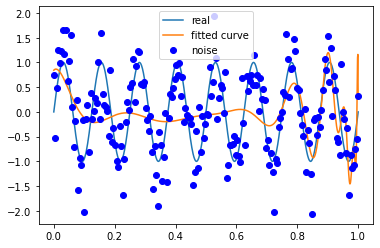
拟合效果与条件关系
多项式次数越高越容易拟合高频的信号,但是多项式次数过高容易过拟合;
多项式次数越低越容易欠拟合,尤其是对于低频信号。
因此需要在尽可能拟合信号的情况下降低多项式次数,从而降低噪声对于模型训练的影响。